FrattaliIntroduzione
Guardando la natura intorno a te, potresti aver notato delle piante intricate come queste:


Questa felce è composta da molte foglie che si ramificano dalla più grande alla più piccola.


Questo broccolo romanesco è costituito da
Inizialmente, queste forme sembrano molto complesse, ma quando le guardi più da vicino, potresti notare che entrambe seguono uno schema relativamente semplice: tutte le singole parti della pianta assomigliano all’intera pianta in miniatura. Lo stesso modello viene ripetuto più e più volte, su scale sempre più piccole.
In matematica, questa proprietà si chiama auto-somiglianza e queste forme sono note come
Per creare i frattali, dobbiamo iniziare con un modello semplice e quindi ripeterlo più e più volte, su scale sempre più piccole.
Uno dei modelli più semplici potrebbe essere un segmento, con altri due segmenti che si diramano da un'estremità. Se ripetiamo questo schema, entrambi i segmenti blu avranno altri due rami alle estremità.
Puoi spostare i punti blu per modificare la lunghezza e l'angolo di tutti i rami. Poi aumenta il numero di iterazioni utilizzando
A seconda della posizione dei rami, puoi creare motivi completamente diversi - che assomigliano alla sopra, ad un o a dei . Cos'altro puoi trovare?
Un altro frattale famoso è il
Nota che la forma finale è composta da tre copie identiche di se stessa, e ognuna di queste è costituita da copie ancora più piccole dell'intero triangolo! Puoi guardare il triangolo sempre più da vicino, e notare come i motivi e le forme continuano a ripetersi.
Le piante all'inizio di questo capitolo sembrano proprio ai frattali, ma è chiaramente impossibile creare dei veri frattali nella vita reale. Se continuiamo a ripetere lo stesso schema più e più volte, in scale sempre più piccole, arriveremmo a cellule, molecole o atomi che non possono essere divisi ulteriormente.
Tuttavia, usando la matematica, possiamo riflettere sulle proprietà dei veri frattali e scoprire che sono davvero sorprendenti...
Dimensioni Frattali
Innanzitutto, pensiamo alla dimensione dei frattali. Una linea ha
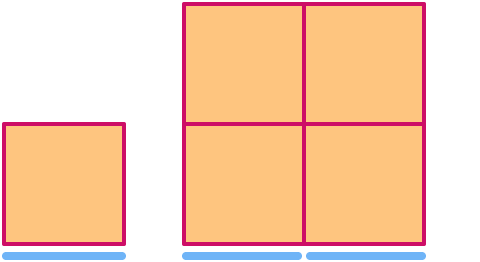
Un quadrato ha
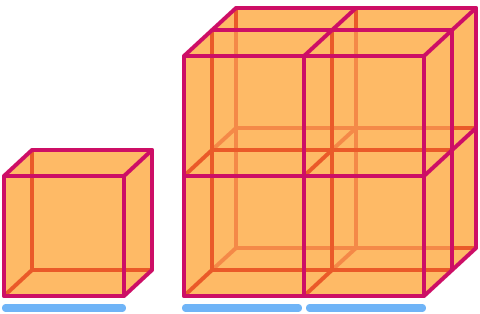
Un cubo ha
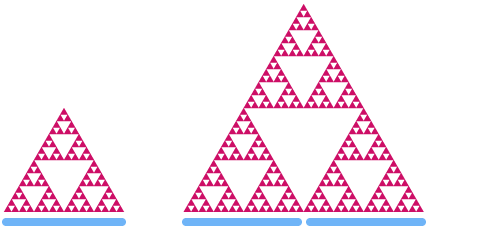
Ora diamo un'occhiata al triangolo di Sierpinski. Se lo ingrandiamo di un fattore 2, puoi vedere che la sua "area" aumenta di un fattore di
Supponiamo che d sia la dimensione del triangolo di Sierpinski. Usando lo stesso modello di cui sopra, otteniamo
Ma aspetta... questa dimensione non è un numero intero! Sembra impossibile, ma questa è solo una delle strane proprietà dei frattali. In effetti, questo è ciò che dà il nome ai frattali: hanno una dimensione frazionaria.
Con ogni iterazione, rimuoviamo parte dell'area del triangolo di Sierpinski. Se potessimo farlo molte volte all'infinito, tutta l'area sarebbe rimossa: ecco perché il triangolo di Sierpinski è qualcosa tra un'area bidimensionale e una linea monodimensionale.
Mentre molti frattali sono auto-simili, una definizione migliore è che i frattali sono forme che hanno una dimensione non intera.
Curva di Koch
Ci sono molte forme in natura che sembrano ai frattali. Abbiamo già visto alcune piante all'inizio di questo capitolo. Altri esempi sono i fiocchi di neve e i cristalli di ghiaccio:
Per creare il nostro fiocco di neve frattale, dobbiamo ancora una volta trovare una semplice procedura da poter applicare più e più volte.
Come per il triangolo di Sierpinski, iniziamo con un singolo triangolo equilatero. Tuttavia, anziché rimuovere i triangoli più piccoli ad ogni passo, li aggiungiamo lungo i lati. La lunghezza del lato di ogni triangolo aggiunto è
La forma risultante si chiama
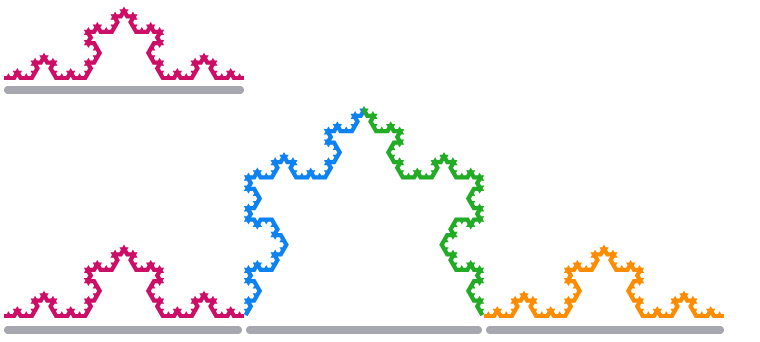
Quando ingrandiamo un segmento della curva di Koch di un fattore 3, la sua lunghezza
Usando la stessa relazione tra dimensioni e fattori di scala come sopra, otteniamo l'equazione
Area
La creazione dei fiocchi di neve di Koch è quasi come una




Dopo la prima iterazione, il numero di nuovi triangoli aggiunti aumenta di un fattore
Supponiamo che il
Utilizzando la formula per la somma di infinite
Perimetro
Possiamo anche provare a calcolare il perimetro del fiocco di neve di Koch. Come abbiamo già visto prima, la lunghezza del perimetro cambia di un fattore pari a
Ciò significa che, ancora una volta, abbiamo una serie geometrica, ma in questo caso

Se questo ti sembra controintuitivo, ricorda che moltiplichiamo il perimetro di
È incredibile avere una forma con un'area finita e un perimetro infinito - ma questa è solo una delle tante proprietà inattese dei frattali.
Puoi trovare altri modi per creare i tuoi frattali?
"My soul is spiralling on frozen fractals all around." (Traduzione: La mia anima sta crescendo su frattali congelati tutt'intorno).
Spugna di Menger
I frattali non devono essere "piatti", come molti degli esempi sopra. Uno dei frattali più famosi che sembrano tridimensionali è la spugna di Menger, dal nome del matematico
Iniziamo con un cubo solido ed eseguiamo ripetutamente dei fori sempre più piccoli sui suoi lati. Ogni nuova iterazione ha
Un cubo
Ora possiamo provare a calcolare la dimensione d della spugna di Menger, proprio come abbiamo fatto per la curva di Koch sopra. In questo caso otteniamo
Se immaginassi di tagliare sempre più buchi, per un numero infinito di volte, non rimarrebbe alcun volume effettivo. Ecco perché il cubo "non è proprio" tridimensionale!
Frattali Lungo Le Coste
Una delle caratteristiche chiave di tutti i frattali che abbiamo visto finora è che puoi continuare ad “ingrandirli” e trovare sempre nuovi modelli. Intorno al 1920, il matematico britannico
Inizi con la forma base del paese e, ingrandendo, aggiungi insenature, baie ed estuari dei fiumi, quindi singole scogliere, rocce, ciottoli e così via:
Questo è un problema significativo nel calcolo della lunghezza dei confini di un Paese: come si decide quanto ingrandire e quali angoli e dettagli includere?
Un modo in cui potremmo misurare la lunghezza della costa britannica, ad esempio, è quello di prendere un lungo righello, camminare lungo le spiagge e quindi sommare tutte le distanze.
Se il righello è lungo
Possiamo semplicemente continuare, con righelli sempre più piccoli, e ogni volta il risultato della lunghezza della costa aumenterebbe un po' di più. Proprio come prima con la curva di Koch, sembra che la costa della Gran Bretagna sia infinitamente lunga! Questo è spesso chiamato paradosso della linea costiera.
Qualche decennio più tardi, il matematico
La costa della Gran Bretagna certamente "sembra" frattale, ma non è auto-simile, come altri frattali che abbiamo visto prima. Per trovarne le dimensioni, possiamo disegnarla su una griglia e contare il numero di celle con cui si interseca.
Inizialmente, ci sono 88 celle intersecanti. Se ingrandiamo la costa di un fattore 2, ci sono 197 celle intersecanti - più del doppio!
La dimensione della costa è aumentata di un fattore
Se lo ripetessimo con griglie più grandi, scopriremmo che la dimensione della costa britannica è in realtà circa 1,21. Mandelbrot capì che questa dimensione frattale è anche una misura della rugosità di una forma – un nuovo concetto, che ha trovato importanti applicazioni in molte altre aree della matematica e della scienza.
Tanti Frattali nella Natura e nella Tecnologia
Mentre i veri frattali non possono esistere in natura, ci sono molti oggetti che assomigliano quasi a dei frattali. Abbiamo già visto piante, fiocchi di neve e coste, e qui ci sono altri esempi:
Catena montuosa in Asia centrale
Delta del fiume Gange in India
Fulmine
Vasi sanguigni nella retina
Grand Canyon negli Stati Uniti
Nuvole
Tutti questi oggetti potrebbero apparire completamente casuali, ma proprio come i frattali, c'è un modello sottostante che determina come sono formati. La matematica può aiutarci a capire meglio le forme, e i frattali hanno applicazioni in vari campi, come medicina, biologia, geologia e meteorologia.
Terreno frattale generato al computer
Possiamo anche usare i frattali per creare "copie" realistiche della natura, ad esempio i paesaggi e le superfici usati nei videogiochi o nei film generati al computer. L'acqua, le montagne e le nuvole in questa immagine sono realizzate interamente al computer, con l'aiuto di frattali!
E possiamo persino invertire questo processo per comprimere le immagini digitali, per ridurne le dimensioni. I primi algoritmi sono stati sviluppati da Michael Barnsley e Alan Sloan negli anni '80 e se ne stanno ancora studiando di nuovi.