FrattaliInsieme di Mandelbrot

Tutti i frattali che abbiamo visto nei capitoli precedenti sono stati creati usando un processo di iterazione: inizi con uno schema specifico e poi lo ripeti più e più volte.

Questo è simile ad un altro concetto matematico che hai visto precedentemente: con le sequenze ricorsive

, inizi con un numero specifico, quindi applichi la stessa formula ricorsiva, molte volte, per ottenere il numero successivo nella sequenza.

Prendiamo la formula ricorsiva

come esempio, e tracciamo i suoi termini su una riga numerica. Puoi modificare il valore di x0:

Nota come la sequenza risultante può comportarsi in modo molto diverso, a seconda del valore iniziale x0:

Se x0>1, la sequenza ???

: continua a crescere, fino all'infinito.

Se x0 è compreso tra -1 e 1, la sequenza ???

Se x0<−1, la sequenza ???

Finora non abbiamo imparato nulla di nuovo. Tuttavia, circa un secolo fa, i matematici hanno iniziato ad esplorare cosa succede a queste sequenze se si usano numeri complessi

, invece della linea numerica reale. Le loro scoperte furono alcuni dei risultati più sorprendenti e belli di tutta la matematica.

Insieme di Julia

Usiamo la stessa sequenza di prima,

, ma sul piano complesso. Puoi spostare la posizione di x0, per vedere cosa succede ai seguenti termini. Se la sequenza sembra convergere, coloriamo il punto corrispondente sul piano in blu:

xn=xn−12

x0=

x1=

x2=

x3=

…Diverge!

Come puoi vedere, la sequenza converge finché x0 si trova ???

(il cerchio con raggio 1, centrato sull'origine).

Ora rendiamo le cose un po' più difficili. Anziché calcolare semplicemente il quadrato del numero precedente, aggiungiamo anche una costante c (che può essere qualsiasi numero complesso). In altre parole,

. Pensi che avremo ancora un cerchio di convergenza? Quali altre forme pensi di poter ottenere?

In questo diagramma, puoi spostare la posizione di x0 e il valore di c:

xn=xn−12+

x0=

x1=

x2=

x3=

…Diverge!

Sappiamo già cosa succede se – è lo stesso dell'esempio sopra. La convergenza della sequenza fino a quando x0 si trova all'interno del cerchio unitario.

Non appena cambiamo il valore di c, succede qualcosa di meraviglioso: il cerchio si trasforma in una forma frattale altamente complessa.

Quando , la forma si divide in un’infinità di piccoli elementi disposti a spirale.

In alcuni casi, la sequenza non converge in un punto singolo, ma raggiunge un ciclo di più punti, come un triangolo. Questi cicli sono chiamati orbite.

I punti di colore blu indicano che la sequenza corrispondente converge o ha un'orbita (diciamo che è delimitata). I punti lasciati bianchi significano che la sequenza corrispondente diverge: non è delimitata e alla fine esplode all'infinito.

Cos'altro puoi trovare? Dai un'occhiata agli schemi quando o quando . Ci sono anche alcuni valori di c dove ogni sequenza diverge, quindi l'intero piano complesso rimane bianco.

Le diverse forme che si creano colorando i numeri sono chiamate Insiemi di Julia

. Furono scoperti indipendentemente da due matematici francesi, Gaston Julia e Pierre Fatou, intorno al 1918.

A quel tempo, non c'erano computer per visualizzare l'aspetto degli insiemi di Julia. Matematici come Julia e Fatou sono stati in grado di ragionare matematicamente solo con schizzi e rappresentazioni approssimative disegnate a mano.

Non abbiamo questo problema oggi: tutte le immagini qui sotto sono diversi insiemi di Julia. I diversi colori indicano quanto velocemente la sequenza differisce in ogni punto:

c=−0.70176−0.3842i

c=−0.4+0.6i

c=0.285+0.01i

Insieme di Mandelbrot

Durante la creazione di diversi insiemi di Julia, potresti aver notato che per alcuni valori di c ogni sequenza diverge e l'intero piano complesso rimane bianco. Qualche decennio dopo Julia e Fatou, una nuova generazione di matematici ha cercato di mappare l'aspetto di queste aree.

Nell'esempio precedente, abbiamo scelto un valore fisso per c, quindi abbiamo cambiato la posizione di x0 per colorare il piano. Ora fissiamo il valore di x0=0 e invece cambiamo il valore di c.

Ancora una volta, spostati sul piano complesso per rivelare l'area in cui le sequenze rimangono limitate. Quali forme ti aspetti?

xn=xn−12+

x0=

x1=

x2=

x3=

…Diverge!

Questo frattale è chiamato Insieme di Mandelbrot

e, quando viene ruotato di 90 °, sembra quasi ad una persona, con testa, corpo e due braccia. È stato definito e disegnato per la prima volta in un articolo scientifico del 1978 dei matematici Robert Brooks e Peter Matelski:

Alcuni anni dopo, Benoit Mandelbrot

usò i potenti computer dell’IBM per creare una visualizzazione molto più dettagliata del frattale, che in seguito prese il suo nome. Le prime stampe avevano un aspetto diverso da quello che si aspettava, e poi si rese conto che i tecnici delle stampanti ripulivano la "sfocatura" attorno al bordo, supponendo che fosse causata da particelle di polvere o errori della stampante, mentre invece erano una caratteristica distintiva dei frattali!

Come tutti i frattali, possiamo "ingrandire" il set di Mandelbrot all’infinito, trovando nuovi schemi su ogni scala. Qui puoi ingrandire una parte del set di Mandelbrot che si chiama Cavalluccio Marino. I punti neri sono all'interno dell’insieme di Mandelbrot, dove la sequenza è limitata. I punti colorati sono all'esterno dell'insieme di Mandelbrot, dove la sequenza diverge, e i diversi colori indicano quanto velocemente cresce all'infinito:

Scale:

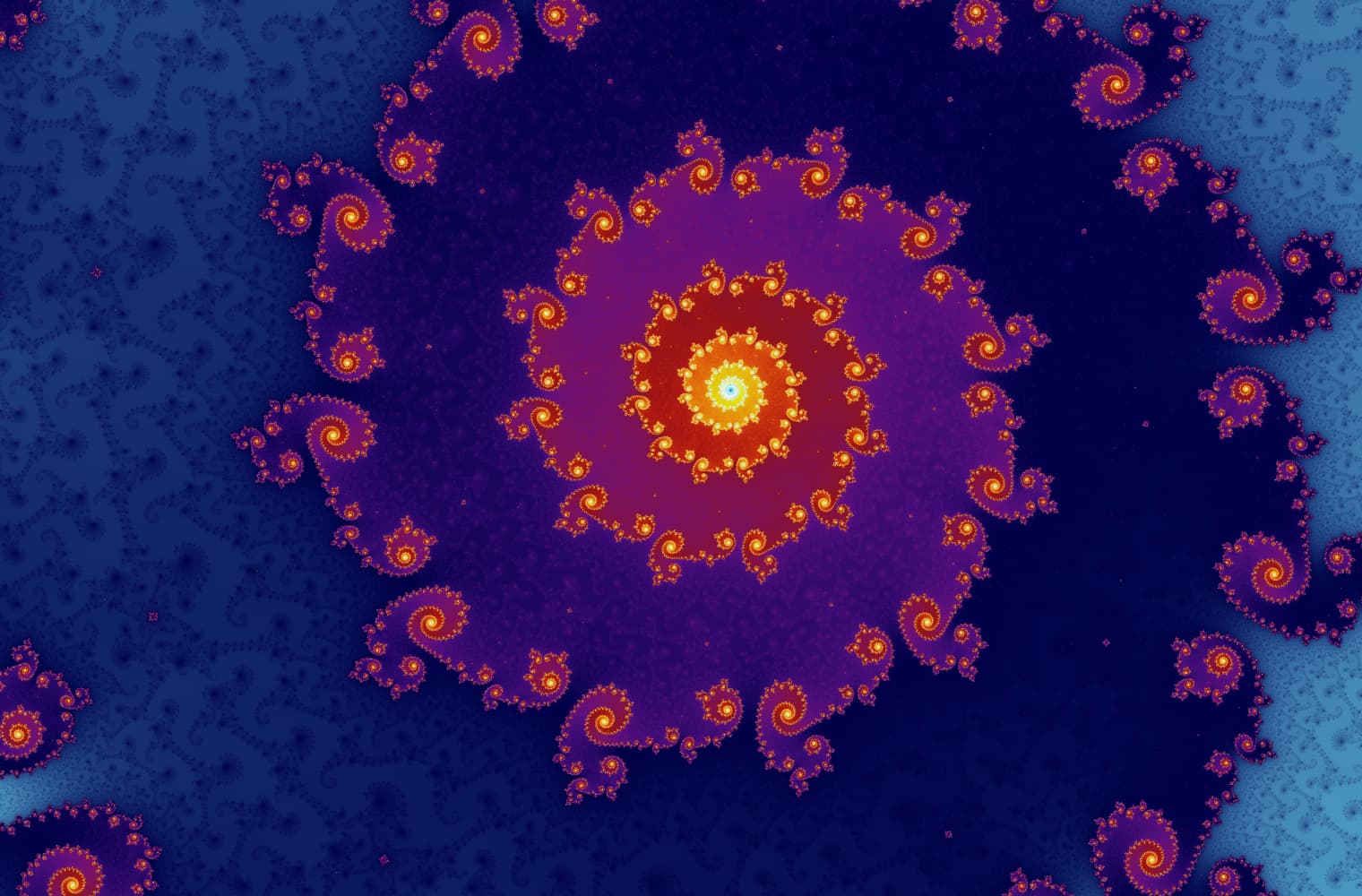
Questa barra di scorrimento è composta da 27 singole immagini, fino ad un livello di zoom di oltre 14 quadrilioni o 254. Complessivamente, ci sono voluti quasi 45 minuti per il rendering su un laptop moderno. Il set di Mandelbrot può essere creato con una sola, semplice equazione,

, ma è infinitamente complesso e straordinariamente bello.

Mentre sposti il valore di c attorno all'insieme di Mandelbrot, potresti notare una proprietà curiosa:

Tutte le sequenze all'interno del corpo principale dell’insieme di Mandelbrot ???
in un singolo punto.
Le sequenze all'interno di questo cerchio grande ???
composta da punti.
Le sequenze in questo cerchio più piccolo hanno orbite di lunghezza .

Ogni cerchio ha un'orbita di dimensioni diverse, e i cerchi più piccoli hanno sempre più punti nelle loro orbite. Le dimensioni di queste orbite sono strettamente correlate alla Mappa Logistica, un concetto importante nella Teoria del Caos.

Bernoit Mandelbrot ha dedicato gran parte della sua vita allo studio dei frattali, così come alla matematica di rugosità e auto-somiglianza. Il suo lavoro ha avuto applicazioni in fisica, meteorologia, neurologia, economia, geologia, ingegneria, informatica e molti altri campi.

Nel 1985, l’insieme di Mandelbrot è apparso sulla copertina della rivista Scientific American, e da allora è diventato una delle forme matematiche più riconoscibili al mondo. Puoi trovarlo su magliette, video musicali e come screen saver, ed è stato citato in molti libri e film famosi.