Trasformazioni e simmetriaGruppi e sfondi di simmetria
Alcune forme hanno più di una simmetria - diamo un'occhiata al








Hai già mostrato sopra che un quadrato ha
Ha anche una simmetria rotazionale di
E infine, possiamo pensare di "non fare nulla" come un altro tipo speciale di simmetria, perché il risultato è (ovviamente) lo stesso di prima. Questa è talvolta chiamata identità.
In totale, abbiamo trovato
Ora possiamo davvero iniziare a fare un po 'di aritmetica con queste simmetrie. Ad esempio, possiamo aggiungere due simmetrie per ottenerne di nuove:






Ogni volta che aggiungi due simmetrie di un quadrato, tu prendine uno nuovo. Ecco un "calcolatore di simmetria" in cui puoi provarlo tu stesso:
Passa un po 'di tempo a giocare con il calcolatore di simmetria e prova a trovare eventuali schemi. Puoi completare queste osservazioni?
- L'aggiunta di due rotazioni darà sempre a
(o identità). - L'aggiunta di due riflessioni darà sempre a
(o identità). - L'aggiunta delle stesse due simmetrie nell'ordine opposto
diverso. - L'aggiunta dell'identità
.
Potresti aver già capito che l'aggiunta di simmetrie è in realtà molto simile all'aggiunta di numeri interi:
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
In matematica, qualsiasi raccolta che abbia queste proprietà è chiamata
Ad esempio, i gruppi di simmetria di molecole diverse possono aiutare gli scienziati a prevedere e spiegare le proprietà dei materiali corrispondenti. I gruppi possono anche essere utilizzati per analizzare la strategia vincente nei giochi da tavolo, il comportamento dei virus in medicina, diverse armonie nella musica e molti altri concetti ...
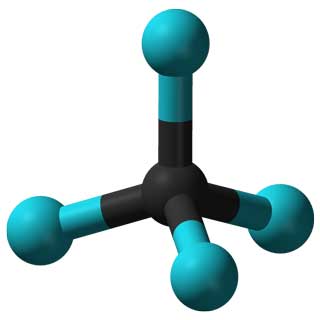
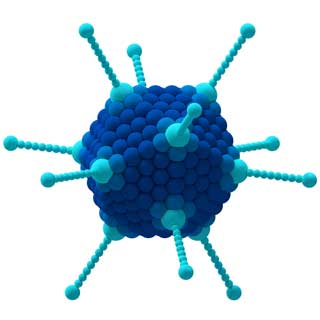
Le proprietà della molecola CCl 4 (a sinistra) e l'Adenovirus (a destra) sono determinati dalle loro simmetrie.
Gruppi di sfondi
Nelle sezioni precedenti abbiamo visto due diversi tipi di simmetria corrispondenti a due diverse trasformazioni: rotazioni e riflessioni. Ma esiste anche una simmetria per il terzo tipo di trasformazione rigida:


Honyecomb esagonale


Piastrelle per pareti in ceramica
Oltre alla simmetria riflessiva, rotazionale e traslazionale, esiste anche un quarto tipo:


Un modello può avere più di un tipo di simmetria. E proprio come per i quadrati, possiamo trovare il
Questi gruppi non ti dicono molto su come appare il modello (ad esempio i suoi colori e forme), come è ripetuto. Più modelli diversi possono avere lo stesso gruppo di simmetria, purché siano disposti e ripetuti allo stesso modo.


Questi due motivi hanno le stesse simmetrie, anche se sembrano molto diversi. Ma le simmetrie non riguardano i colori o le forme superficiali.


Questi due motivi hanno anche le stesse simmetrie - anche se sembrano più simili ai modelli corrispondenti a sinistra, che tra loro.
Si scopre che, mentre ci sono infiniti schemi possibili, tutti hanno uno dei soli 17 diversi gruppi di simmetria. Questi sono chiamati gruppi di sfondi. Ogni gruppo di sfondi è definito da una combinazione di traduzioni, rotazioni, riflessi e riflessi di planata. Riesci a vedere i

Type P1
Only translations

Type P2
Rotations of order 2, translations

Type P3
Rotations of order 3 (120°), translations

Type P4
Four rotations of order 2 (180°), translations

Type P6
Rotations of order 2, 3 and 6 (60°), translations

Type PM
Parallel axes of reflection, translations

Type PMM
Perpendicular reflections, rotations of order 2, translations

Type P4M
Rotations (ord 2 + 4), reflections, glide reflections, translations

Type P6M
Rotations (ord 2 + 6), reflections, glide reflections, translations

Type P3M1
Rotations of order 3, reflections, glide reflections, translations

Type P31M
Rotations of order 3, reflections, glide reflections, translations

Type P4G
Rotations (ord 2 + 4), reflections, glide reflections, translations

Type CMM
Perpendicular reflections, rotations of order 2, translations

Type PMG
Reflections, glide reflections, rotations of order 2, translations

Type PG
Parallel glide reflections, translations

Type CM
Reflections, glide reflections, translations

Type PGG
Perpendicular glide reflections, rotations of order 2, translations
Sfortunatamente non esiste un semplice motivo per cui ci sono 17 di questi gruppi. Dimostrarlo richiede matematica molto più avanzata ...
Invece, puoi provare a disegnare i tuoi motivi ripetuti per ciascuno dei 17 gruppi di sfondi:
Examples of other students’ drawings



I gruppi di carte da parati riguardavano modelli piatti e bidimensionali. Possiamo fare qualcosa di simile per i modelli tridimensionali: questi sono chiamati gruppi cristallografici e ce ne sono 219!
Oltre alle traduzioni, riflessioni, rotazioni e riflessi di planata, questi gruppi includono simmetrie come planimetrie di planata e assi di vite (pensa al movimento quando sviti una bottiglia).
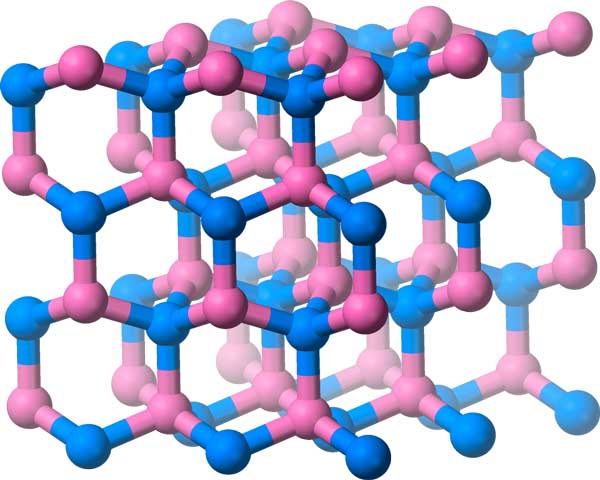
Il nitruro di boro ha le sue molecole disposte in questo reticolo cristallino, che ha un gruppo di simmetria tridimensionale.