English
عربى
中文
Deutsch
Español
Français
हिन्दी
Hrvatski
Italiano
日本語
Português
Română
Русский
Svenska
Türkçe
Tiếng ViệtPoligoni e poliedriSolidi platonici
All'inizio di questo corso abbiamo definito i Un poligono regolare è un poligono in cui tutti i lati hanno la stessa lunghezza e tutti gli angoli interni hanno le stesse dimensioni.
In un poliedro regolare tutte le Le faccedi un poliedro sono i poligoni che compongono la sua superficie. Gli "angoli" di un poliedro sono chiamati vertici. Un solido platonico è un poliedro in cui ogni faccia è un poligono regolare con lo stesso numero di bordi e in cui lo stesso numero di facce si incontrano in ogni vertice. Esistono solo cinque diversi solidi platonici: il tetraedro, il cubo, l'ottaedro, il dodecaedro e l'icosaedro. Platone (c. 425 - 347 a.C.) era un filosofo dell'antica Grecia e, insieme al suo insegnante Socrate e al suo studente Aristotele, gettò le basi stesse della filosofia e della scienza occidentale. Platone fondò l'Accademia di Atene, la prima istituzione di istruzione superiore nel mondo occidentale. I suoi numerosi scritti su filosofia e teologia, scienza e matematica, politica e giustizia, lo rendono uno dei pensatori più influenti di tutti i tempi.
Allora, come sono fatti i solidi platonici – e quanti ce ne sono? per creare un solido, abbiamo bisogno che almeno
Se creiamo un poliedro in cui tre Un triangolo equilatero è un triangolo in cui tutti e tre i lati hanno la stessa lunghezza.
Se quattro triangoli equilateri si incontrano in ogni vertice, otteniamo un solido platonico diverso. È chiamato ottaedro e ha
Se
Se
E nemmeno sette o più triangoli che si incontrano in ogni vertice possono produrre un nuovo poliedro: non c'è abbastanza spazio attorno ad ogni vertice, per accostare così tanti triangoli.
Questo significa che abbiamo trovato
Se
Se
Proviamo ora con il pentagono regolare:
Se
Come prima, quattro o più pentagoni
Il prossimo poligono regolare con cui provare è l'esagono:
Se tre esagoni si incontrano in ogni vertice, otteniamo immediatamente
Lo stesso vale per tutti i poligoni regolari con più di sei lati. Non possono formare una tassellazione, e certamente non possono formare un poligono tridimensionale.
Questo significa che ci sono solo
tetraedro
cubo
ottaedro
dodecaedro
icosaedro
Osserva come il numero di facce e di vertici è QUALUNQUE COSA
Possiamo trasformare un poliedro nel suo poliedro duale, “rimpiazzando” ogni faccia con un vertice, e ogni vertice con una faccia. Queste animazioni mostrano come:
Il tetraedro è il duale di se stesso. Siccome ha lo stesso numero di facce e vertici, scambiarli non cambierebbe nulla.
Platone (c. 425 - 347 a.C.) era un filosofo dell'antica Grecia e, insieme al suo insegnante Socrate e al suo studente Aristotele, gettò le basi stesse della filosofia e della scienza occidentale. Platone fondò l'Accademia di Atene, la prima istituzione di istruzione superiore nel mondo occidentale. I suoi numerosi scritti su filosofia e teologia, scienza e matematica, politica e giustizia, lo rendono uno dei pensatori più influenti di tutti i tempi.
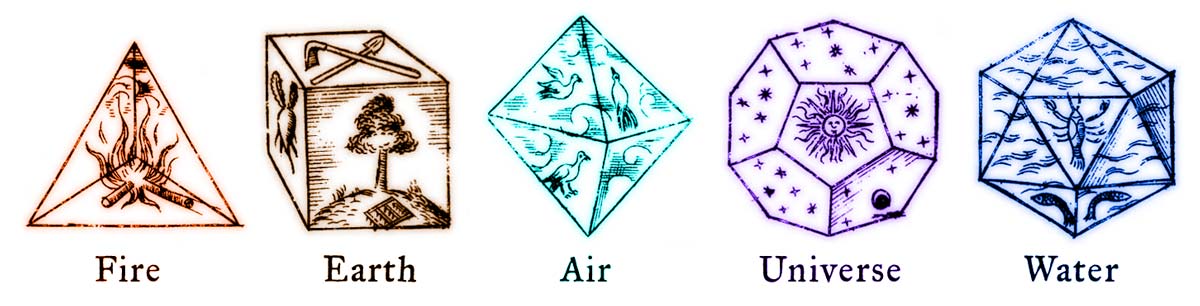
Immagini dal libro di Giovanni Keplero “Harmonices Mundi” (1619)
Solidi di archimede
I solidi platonici sono poliedri particolarmente importanti, ma ne esistono molti altri.
Anche i Un solido di Archimede è un poliedro composto da diversi tipi di poligoni regolari, che sembra lo stesso da ogni direzione. Esistono 13 diversi solidi di Archimede. Un poligono regolare è un poligono in cui tutti i lati hanno la stessa lunghezza e tutti gli angoli interni hanno le stesse dimensioni. Archimede (c. 287 - 212 a.C.) era un antico scienziato e ingegnere greco e uno dei più grandi matematici di tutti i tempi. Ha scoperto molti concetti di calcolo e ha lavorato in geometria, analisi e meccanica. Durante un bagno, Archimede scoprì un modo per determinare il volume di oggetti irregolari utilizzando la quantità di acqua che spostano quando sono immersi. Era così eccitato da questa scoperta che corse per strada, ancora nudo, urlando “Eureka!” (in greco per “L'ho trovato!”). Come ingegnere, costruì ingegnose macchine da difesa durante l'assedio della sua città natale, Siracusa, in Sicilia. Dopo due anni, i romani riuscirono finalmente ad entrare e Archimede fu ucciso. Le sue ultime parole sono state "Non rovinare i miei disegni" - che stava studiando in quel momento.
Tetraedro troncato 8 facce, 12 vertici, 18 spigoli
Cubottaedro 14 facce, 12 vertici, 24 spigoli
Cubo troncato 14 facce, 24 vertici, 36 spigoli
Ottaedro troncato 14 facce, 24 vertici, 36 spigoli
Rombicubottaedro 26 facce, 24 vertici, 48 spigoli
Cubottaedro troncato 26 facce, 48 vertici, 72 spigoli
Cubo camuso 38 facce, 24 vertici, 60 spigoli
Icosidodecaedro 32 facce, 30 vertici, 60 spigoli
Dodecaedro troncato 32 facce, 60 vertici, 90 spigoli
Icosaedro troncato 32 facce, 60 vertici, 90 spigoli
Rhombicosidodecaedro 62 facce, 60 vertici, 120 spigoli
Icosidodecaedro troncato 62 facce, 120 vertici, 180 spigoli
Dodecaedro camuso 92 facce, 60 vertici, 150 spigoli
Applicazioni
Platone si sbagliava nel pensare che tutti gli elementi consistessero in solidi poatonici, ma i poliedri regolari hanno molte proprietà particolari grazie alle quali appaiono altrove in natura – e possiamo sfruttare queste proprieta nella scienza e nell'ingenieria.
Scheledro di radiolario
Virus icosaedrico
Molti virus, batteri e altri piccoli organismi hanno la forma di un L'Iosaedro__ è un solido platonico ed è composto da 20 facce che sono tutti triangoli equilateri. Ha 12 vertici e 30 bordi.
Molecola di buckminsterfullerene
Biosfera di Montreal
Molte molecole hanno la forma di poliedri regolari. L'esempi più famoso è il Il Icosaedro troncato è un solido di Archimede composto da 12 pentagoni regolari e 20 esagoni regolari.
È stata scoperta nel 1985 mentre gli scienziati ricercavano le polveri interstellari. La chiamarono “Buckyball” (o Buckminsterfullerene) in onore dell'architetto Richard Buckminster "Bucky" Fuller (1895-1983) era un architetto, designer e inventore americano. È famoso per la costruzione di cupole geodetiche - grandi strutture sferiche. Alle molecole di carbonio dall'aspetto simile a queste cupole, i fullereni, venne attribuito il suo nome.
Ottaedro di fluorite
Cubo di pirite
La maggior parte dei cristalli hanno i loro atomi disposti in una griglia regolare composta da Il Tetrahedron è un solido platonico ed è composto da quattro facce che sono triangoli equilateri. Ha quattro vertici e sei bordi. Un cubo(a volte chiamato Hexahedron) è un poliedro normale in cui ogni faccia è un quadrato. È uno dei cinque solidi platonici e ha 6 facce, 8 vertici e 12 spigoli. Il Ottaedro è un solido platonico ed è composto da 8 facce che sono triangoli equilateri. Ha 6 vertici e 12 bordi.
Strutture reticolari
Museo del Louvre a Paris
I tetraedri e gli ottaedri sono incredibilmente rigidi e stabili, il che li rende molto utili nelle construzioni. strutture reticolari sono delle strutture poligonali che possono sostenere ampi tetti e pesanti ponti.
Pallone da calcio
Dado poligonale
I solidi platonici, sono anche usati per creare dei dadi. A causa della loro simmetria, ogni faccia ha la stessa Una probabilitàè un numero compreso tra 0 e 1 che indica la probabilità che si verifichi un determinato evento. La probabilità di un evento A è scritta come
L' Il Icosaedro troncato è un solido di Archimede composto da 12 pentagoni regolari e 20 esagoni regolari.