Sequenze e patternSuccessioni aritmetiche e geometriche

Nel 1682, l'astronomo Edmond Halley osservò un fenomeno insolito: un oggetto bianco splendente con una lunga coda che si muoveva attraverso il cielo notturno. Era una cometa, una piccola roccia ghiacciata che vola nello spazio, lasciando dietro di sé una scia di polvere e ghiaccio.

Halley ricordò che altri astronomi avevano osservato comete simili molto prima: una nel 1530 e un'altra nel 1606. Notate che l'intervallo tra due osservazioni consecutive è lo stesso, in entrambi i casi: anni.

Immagine della cometa di Halley,
fotografata nel 1986 nell'Isola di Pasqua

Halley concluse che tutte e tre le osservazioni erano in effetti della stessa cometa - che ora viene chiamata la cometa di Halley. Orbita intorno al sole e passa la Terra circa ogni 76 anni. L'astronomo riuscì anche a predire quando la cometa sarà visibile in futuro:

1530, 1606*{span.arrow}+76*, 1682*{span.arrow}+76*, 1758*{span.arrow}+76*, +76, +76, +76, …

In realtà, l'intervallo di tempo non è sempre esattamente di 76 anni: può variare di uno o due anni, poiché l'orbita della cometa viene interrotta da altri pianeti. Oggi sappiamo che la cometa di Halley fu osservata dagli antichi astronomi già nel 240 a.C.!

Raffigurazioni della cometa di Halley nel tempo: una tavoletta babilonese (164 a.C.), un arazzo medievale (1070), una rivista scientifica (1910) e un francobollo sovietico (1986).

Un altro gruppo di scienziati sta studiando il comportamento di una palla da tennis che rimbalza. Hanno lasciato cadere la palla da un'altezza di 10 metri e hanno misurato la sua posizione nel tempo. Ad ogni rimbalzo, la palla perde parte della sua altezza originale:

Gli scienziati hanno notato che la palla perde il 20% della sua altezza dopo ogni rimbalzo. In altre parole, l'altezza massima di ogni rimbalzo è dell'80% di quella precedente. Ciò ha permesso loro di prevedere l'altezza di ogni rimbalzo successivo:

10, 8*{span.arrow}×0.8*, ×0.8, ×0.8, 4.096*{span.arrow}×0.8*, 3.277*{span.arrow}×0.8*, 2.621*{span.arrow}×0.8*, 2.097*{span.arrow}×0.8*, …

Definizioni

Se confronti entrambi questi problemi, potresti notare che ci sono molte somiglianze: la sequenza della cometa di Halley ha la stessa tra termini consecutivi, mentre la sequenza di rimbalzi della pallina da tennis ha lo stesso tra termini consecutivi.

Le successioni con queste proprietà hanno un nome speciale:

Una progressione aritmetica ha una differenza costante d tra termini consecutivi.

Lo stesso numero viene aggiunto o sottratto ad ogni termine, per produrre quello successivo.

Una progressione geometrica ha un rapporto r costante tra termini consecutivi.

Ogni termine viene moltiplicato o diviso per lo stesso numero, per produrre il prossimo.

Ecco varie progressioni: puoi determinare quali sono aritmetiche, geometriche o nessuna delle due, e quali sono i valori di d e r?

2, 4, 8, 16, 32, 64, ...

è , con rapporto .

2, 5, 8, 11, 14, 17, ...

è , con differenza .

17, 13, 9, 5, 1, –3, ...

è , con differenza .

2, 4, 7, 11, 16, 22, ...

è .

40, 20, 10, 5, 2,5, 1,25, ...

è , con rapporto .

Per definire una progressione aritmetica o geometrica, dobbiamo conoscere non solo la differenza o il rapporto costante, ma anche il valore iniziale (chiamato a). Qui puoi generare le tue progressioni e tracciare i loro valori su un grafico, modificando i valori di a, d e r. Riesci a trovare degli schemi?

Progressione aritmetica

a = ${a}, d = ${d}

${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …

Progressione geometrica

a = ${b}, r = ${r}

${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …

Hai notato che tutte le progressioni aritmetiche sembrano molto simili? Se la differenza è positiva, costantemente e se la differenza è negativa, costantemente.

Le progressioni geometriche, invece, possono comportarsi in modo completamente diverso in base ai valori di a e r:

Se , i termini , fino all'infinito. I matematici affermano che la progressione diverge.

Se , i termini . Diciamo che la progressione converge.

o Se , i termini si alternano tra positivo e negativo, mentre il loro aumenta.

Imparerai di più sulla convergenza e la divergenza nella ultima sezione di questo corso.

Formule ricorsive ed esplicite

Nella sezione precedente, hai appreso che una formula ricorsiva ci dice il valore di ciascun termine in funzione dei termini precedenti. Ecco le formule ricorsive per progressioni aritmetiche e geometriche:

xn=

Un problema con le formule ricorsive è che per trovare il 100° termine, ad esempio, dobbiamo prima calcolare i 99 termini precedenti e ciò potrebbe richiedere molto tempo. Invece, possiamo provare a trovare una formula esplicita, che ci dice direttamente il valore di n.

Per progressioni aritmetiche, dobbiamo aggiungere d ad ogni passaggio:

x1= a

x2= a+d

x3= a+d+d

x4=

x5=

All' ennesimo termine, stiamo aggiungendo copie di d, quindi la formula generale è

xn=a+d×n−1.

Per progressioni geometriche, dobbiamo moltiplicare r ad ogni passaggio:

x1=a

x2=a×r

x3=a×r×r

x4=

x5=

All' ennesimo termine, stiamo moltiplicando copie di r, quindi la formula generale è

xn=a×rn−1.

Ecco un riepilogo di tutte le definizioni e le formule che hai visto finora:

Una progressione aritmetica ha il primo termine a e la differenza costante d tra termini consecutivi.

Formula ricorsiva: xn=xn−1+d

Formula esplicita: xn=a+d×n−1

Una progressione geometrica ha il primo termine a e il rapporto costante r tra termini consecutivi.

Formula ricorsiva: xn=xn−1×r

Formula esplicita: xn=a×rn−1

Ora diamo un'occhiata ad alcuni esempi in cui possiamo usare tutto questo!

Passa un favore

Ecco una breve clip del film Un sogno per domani (Pay It Forward), in cui Trevor, 12 anni, spiega la sua idea per rendere il mondo un posto migliore:

L'essenza dell'idea di Trevor è che, se tutti "passano un favore", una sola persona può avere un impatto enorme sul mondo:

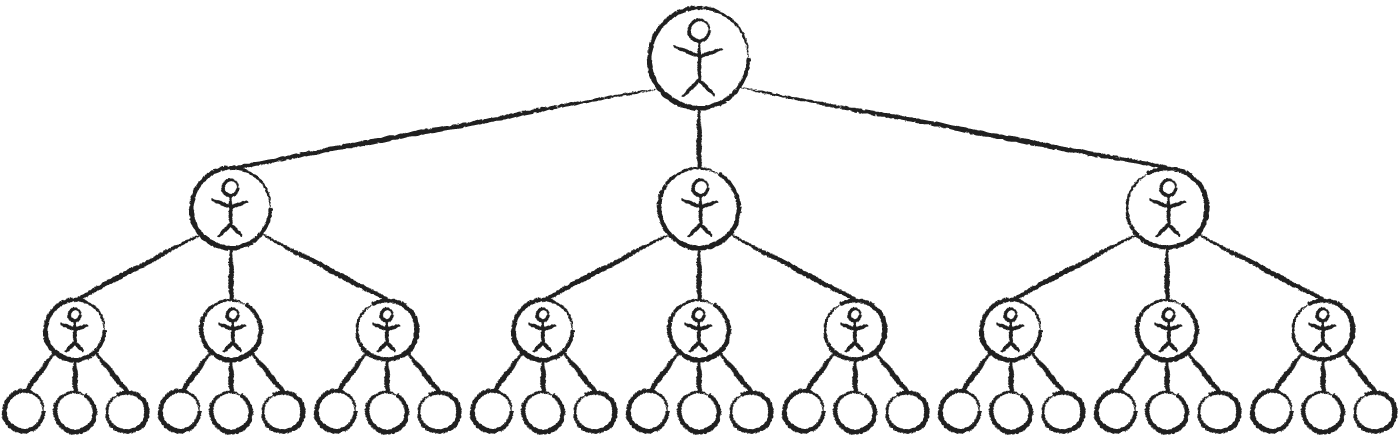
Notiamo come il numero di persone in ogni fase forma , con rapporto costante :

1, 3*{span.arrow}×3*, 9*{span.arrow}×3*, ×3, ×3, ×3, …

Utilizzando la formula esplicita per le progressioni geometriche, possiamo capire quante nuove persone sono interessate in qualsiasi fase:

xn =

Il numero di persone aumenta incredibilmente in fretta. Nel decimo passaggio, raggiungiamo 19 683 nuove persone, e dopo 22 passaggi vengono coinvolte più persone di quelle che attualmente vivono sulla Terra.

Questa successione di numeri ha un nome speciale: la potenza di 3. Come puoi vedere, ogni termine è in realtà solo una diversa potenza di 3:

30, 31, 32, 33, 34, 35, ...

Chi vuole essere milionario?

DISPONIBILE A BREVE!

Il problema della scacchiera

DISPONIBILE A BREVE!

Cambia lingua

Accedi a Mathigon

Condividere

Ripristina avanzamento

Glossario