Sequenze e patternSuccessione di Fibonacci
Immagina di aver ricevuto un paio di coniglietti, un maschio e una femmina. Sono conigli molto speciali, perché non muoiono mai, e la femmina dà alla luce una nuova coppia di conigli esattamente una volta al mese (sempre un'altra coppia di maschi e femmine).




















Nel mese successivo avresti avuto 13 coppie di conigli: gli 8 del mese precedente, più 5 nuove coppie. Riesci a rilevare un modello in questa successione?
Il numero di conigli in un determinato mese è
Riesci a calcolare il numero di conigli dopo qualche mese?
1, 1, 2, 3, 5, 8,
Quindi dopo 12 mesi avrai 144 coppie di conigli!
Questa sequenza di numeri è chiamata
Quando Fibonacci nacque nel 1175, la maggior parte delle persone in Europa utilizzava ancora il
Al suo ritorno in Italia, Fibonacci scrisse un libro intitolato Liber Abaci (latino per "Libro del calcolo"), dove introdusse per la prima volta i nuovi numeri arabi ai mercanti europei. Sono stati un successo immediato - e li usiamo ancora oggi.
In una delle pagine del suo libro, ha anche studiato gli schemi genetici dei conigli - ecco perché i numeri di Fibonacci hanno preso il suo nome.
Pagine del libro Liber Abaci di Fibonacci
Naturalmente, in realtà i conigli si riproducono in modo diverso. Non hanno esattamente un figlio maschio e una femmina ogni mese, e non abbiamo mai tenuto conto della morte dei conigli.
Ma si scopre che ci sono molti altri luoghi in natura in cui compaiono i numeri di Fibonacci: ad esempio le spirali nelle piante. Riesci a contare quante spirali ci sono in ogni direzione?
Questa pigna ha
Questo girasole ha 34 spirali in senso orario e 55 spirali in senso antiorario.
In entrambi i casi, i numeri delle spirali sono numeri di Fibonacci consecutivi. Lo stesso vale per molte altre piante: la prossima volta che esci, conta il numero di petali in un fiore o il numero di foglie su uno stelo. Molto spesso scoprirai che sono numeri di Fibonacci!
Certo, questa non è solo una coincidenza. C'è un motivo importante per cui alla natura piace la successione di Fibonacci! In seguito scoprirai molti più dettagli.
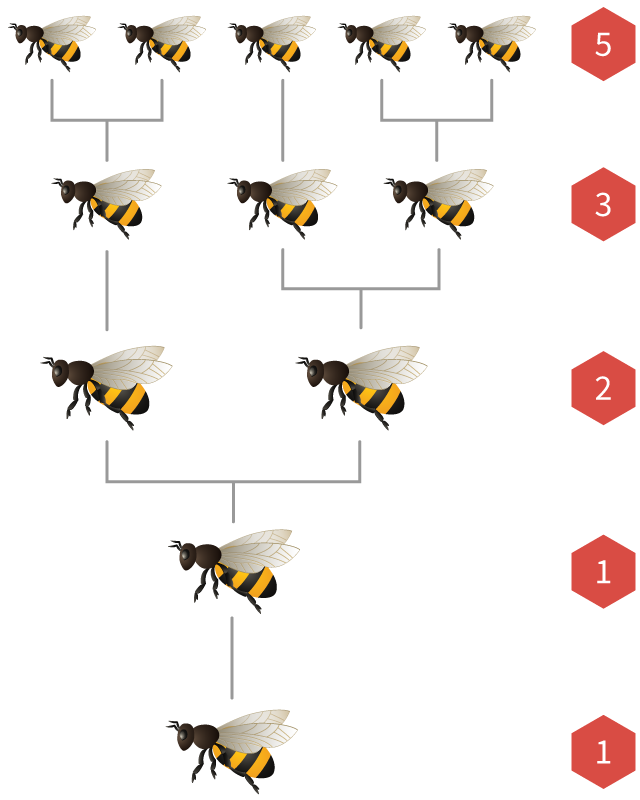
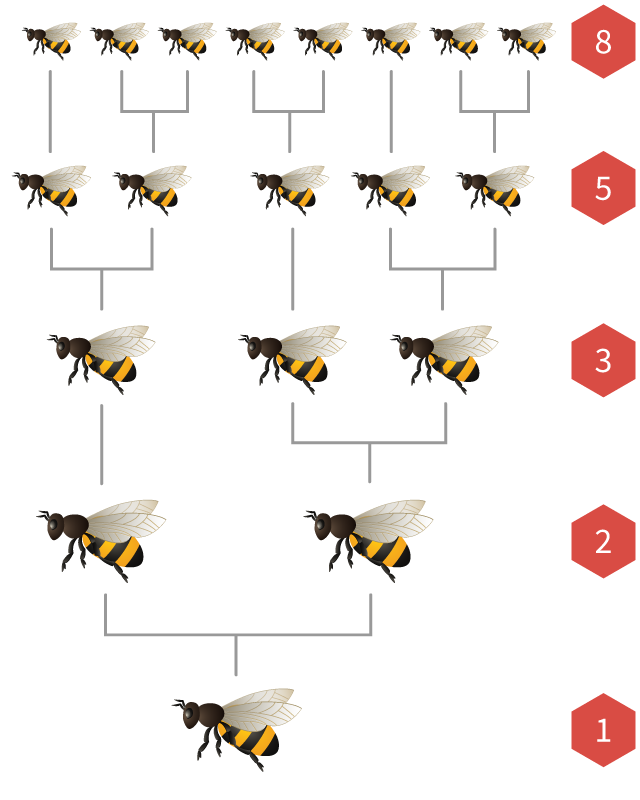
I numeri di Fibonacci compaiono anche nelle popolazioni di api mellifere.
In ogni colonia di api c'è una sola regina che depone molte uova. Se un uovo viene fecondato da un'ape maschio, si schiude in un'ape femmina. Se non viene fertilizzato, si schiude in un'ape maschio (chiamata drone).
Ciò significa che le api femmine hanno
Se disegniamo l'albero genealogico di un'ape, il numero di genitori, nonni, bisnonni e generazioni precedenti sono sempre numeri di Fibonacci!
Occasionalmente, le giovani api femmine vengono alimentate con cibo speciale chiamato "pappa reale". In tal caso, si trasformano in regine e voleranno via per iniziare un nuovo alveare.
La Sezione Aurea
Proprio come il
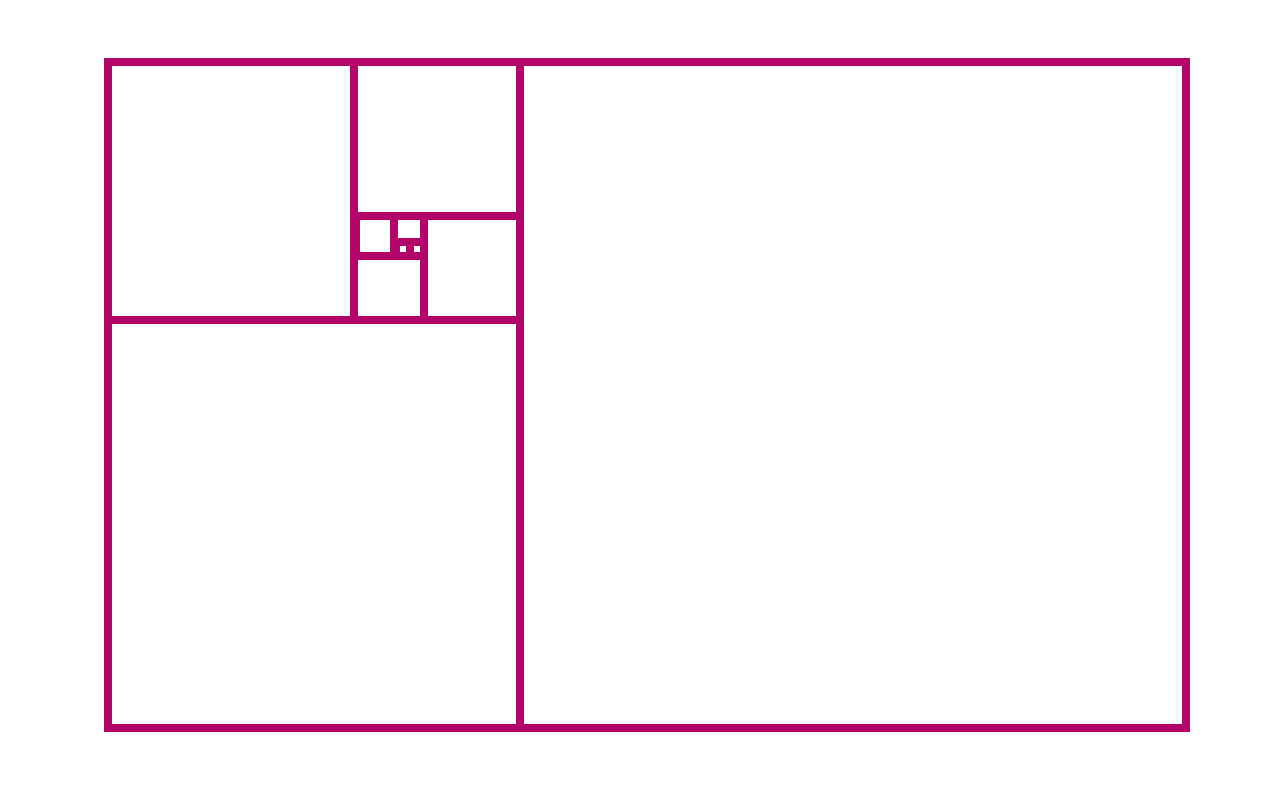
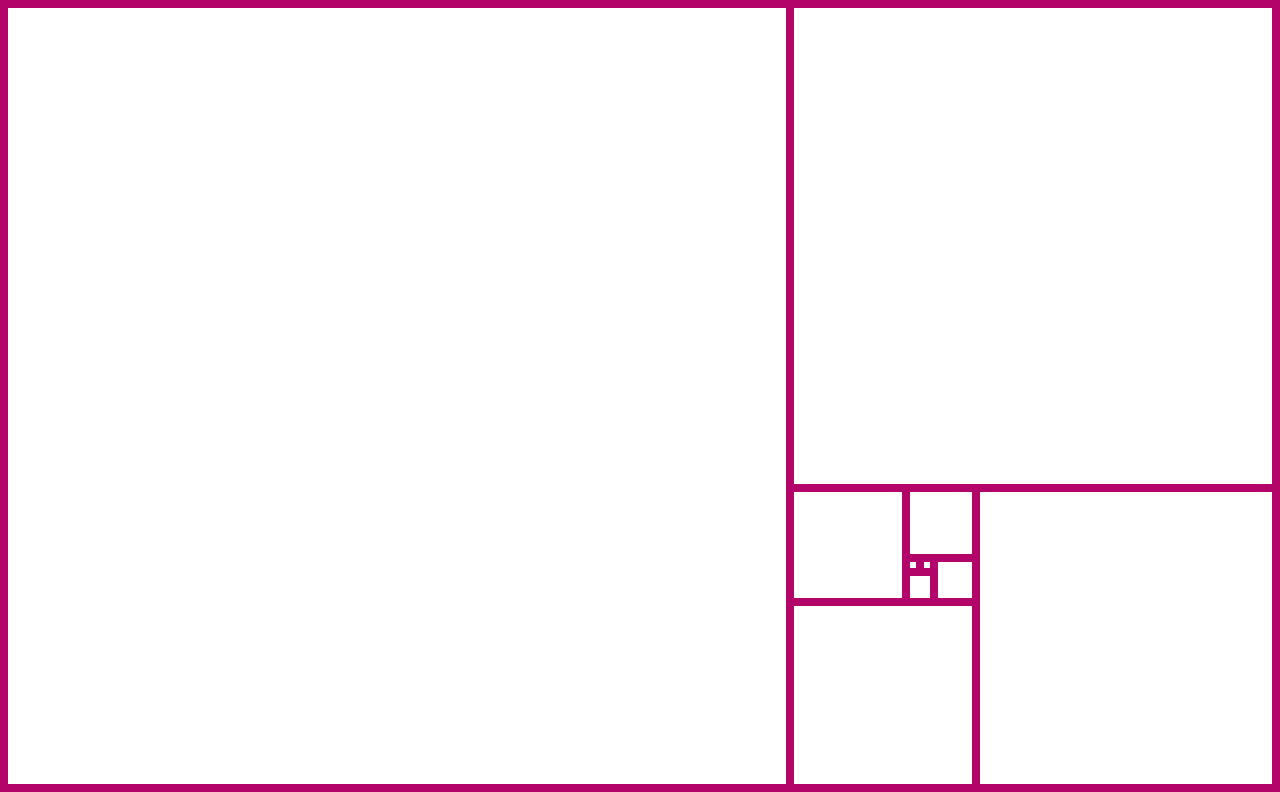
Ad ogni passo, i quadrati formano un rettangolo più grande. La sua larghezza e altezza sono sempre due numeri di Fibonacci consecutivi. Notate il rapporto tra larghezza e altezza dei rettangoli:
Notate che man a mano che si aggiungono più quadrati, le proporzioni sembrano avvicinarsi sempre più a un numero specifico intorno a 1,6. Questo numero è chiamato
Molte persone credono che la sezione aurea sia esteticamente gradevole. Ecco perché viene spesso utilizzata da artisti e architetti, come in questi due esempi:
Si dice che lo scultore greco Fidia abbia usato la sezione aurea durante la progettazione del Partenone ad Atene. La prima lettera del suo nome,
L'ultima cena, dell'artista spagnolo Salvador Dalí, è uno dei tanti dipinti che usa la sezione aurea. Sullo sfondo, puoi anche vedere un grande
Possiamo approssimare la sezione aurea
Tuttavia, si scopre che il valore esatto di
Spirali di Fibonacci
La sezione aurea spiega perché i numeri di Fibonacci compaiono in natura, come il girasole e la pigna che hai visto all'inizio di questa sezione.
Entrambe queste piante crescono verso l'esterno dal loro centro (una parte della pianta chiamata meristema). I nuovi semi, foglie o petali spingono quelli esistenti verso l'esterno.
Sposta il cursore a destra per visualizzare come cresce una pianta. Notate come ogni foglia che viene aggiunta ha una rotazione diversa dalla precedente. L'angolo tra due foglie consecutive è sempre lo stesso.
È importante che i fiori scelgano un'angolazione adeguata: le foglie o i semi devono essere approssimativamente equidistanti in modo da ottenere la maggior quantità di luce solare e sostanze nutritive. Nel diagramma seguente, puoi esplorare come potrebbe apparire un girasole con angoli diversi tra i suoi semi:
Potresti ricordare da prima che il rapporto di numeri di Fibonacci consecutivi si avvicinano sempre più alla sezione aurea - ed è per questo che, se conti il numero di spirali in una pianta, troverai spesso un numero di Fibonacci.
È importante ricordare che la natura non conosce i numeri di Fibonacci. Inoltre, la natura non è in grado di risolvere equazioni per calcolare il rapporto aureo, ma nel corso di milioni di anni le piante hanno avuto molto tempo per provare diverse angolazioni e scoprire quella migliore.
Le piante e gli animali vogliono sempre crescere nel modo più efficiente, ed è per questo che la natura è piena di schemi matematici regolari.
Fibonachos
Finora abbiamo usato solo l'equazione ricorsiva per i numeri di Fibonacci. In realtà esiste anche un'equazione esplicita, ma è molto più difficile da trovare:
Potremmo anche provare a scegliere diversi punti di partenza per i numeri di Fibonacci. Ad esempio, se iniziamo con 2, 1, ... anziché 1, 1, ... otteniamo una successione chiamata numeri di Lucas.
Si scopre che, qualunque siano i due numeri iniziali scelti, le successioni risultanti condividono molte proprietà. Ad esempio, i rapporti di termini consecutivi sempre
Esistono molti altri enigmi, schemi e applicazioni relativi ai numeri di Fibonacci. Ecco alcuni esempi, che puoi provare tu stesso:
Problem solving
1. Divisibilità di Fibonacci
(a) Quali numeri di Fibonacci sono pari? In che modo sono posizionati lungo la sequenza? Puoi spiegare perché?
(b) Quali numeri di Fibonacci sono divisibili per 3 (o divisibili per 4)? Cosa noti?
2. Somme di Fibonacci
Cosa succede se sommi tre numeri di Fibonacci consecutivi? Puoi spiegare perché?
3. Scale di Fibonacci
Quando sali le scale, puoi fare singoli passi o saltare due passi alla volta. Ciò significa che puoi salire una scala in tanti modi diversi. Ad esempio, se ci sono 5 gradini, hai 8 diverse scelte:
Quante scelte ci sono per le scale con 6, 7 o 8 gradini? Riesci a rilevare un modello? E in che modo questo è legato ai numeri di Fibonacci?
© FoxTrot, by Bill Amend