Triangoli e trigonometriaProprietà dei triangoli
Cominciamo con le cose semplici: un triangolo è una figura chiusa che ha tre lati (che sono
Possiamo classificare i triangoli secondo l'ampiezza dei loro angoli:
Un triangolo rettangolo ha un
Un triangolo ottusangolo ha un
Un triangolo acutangolo ha
Per comodità, contrassegnamo i triangoli sempre nello stesso modo. I vertici vengono indicati con le lettere maiuscole A, B e C, i lati vengono indicati con le lettere minuscole a, b and c, e gli angoli con le lettere greche
Il lato opposto al vertice A si indica con a, e l'angolo vicino ad A si indica con
Le mediane
Qui puoi vedere un triangolo e i
La
Sembrerebbe che le mediane
Le mediane si dividono in rapporto 2:1. Per ognuna delle tre mediane, la distanza tra il vertice e il baricentro è sempre
Il baricentro è anche il “punto di equilibrio” di un triangolo. Disegna un triangolo su un cartoncino, ritaglialo e disegna le tre mediane. Se il disegno è accurato, potrai ora tenere in equilibrio il triangolo sulla punta di una matita, o appenderlo perfettamente orizzontale ad un filo che è attaccato al baricentro:
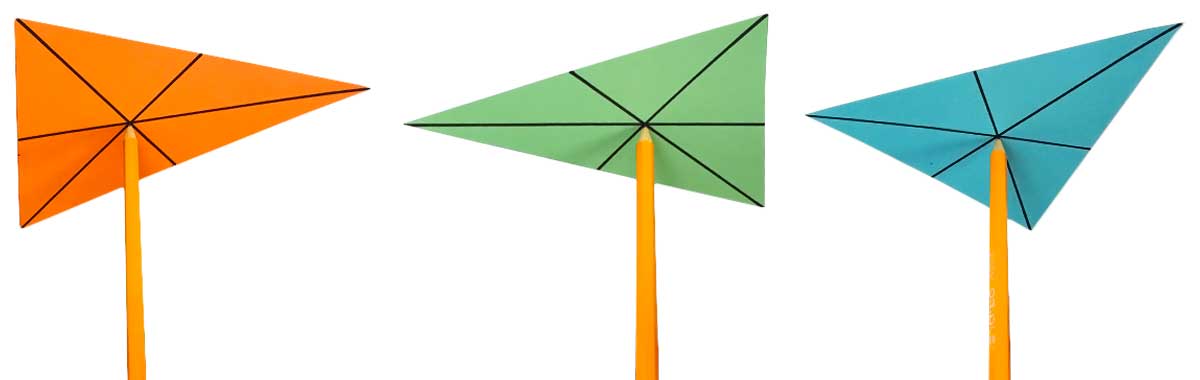
Funziona perché il peso del triangolo è distribuito in modo uniforme attorno al baricentro. In fisica, questo punto è spesso chiamato il centro di massa.
Assi di un triangolo e cerchio circoscritto
Ricorda che l'
Disegna l'asse di tutti e tre i lati di questo triangolo. Per disegnare gli assi di un lato del triangolo, clicca semplicemente su un vertice e trascina il cursore da un vertice all'altro.
Come prima, i tre assi si intersecano in un solo punto. E di nuovo, questo punto ha una proprietà speciale.
Ogni punto su un asse ha la stessa distanza dai due estremi del segmento. Ad esempio, ogni punto sull'asse blu ha la stessa distanza dai punti A e C e ogni punto dell'asse rosso ha la stessa distanza dai punti
Il punto di intersezione giace su tutti e tre gli assi, quindi deve avere la stessa distanza da tutti e tre i
Questo significa che possiamo tracciare un cerchio attorno a questo punto che tocca perfettamente tutti i vertici. Questo cerchio è chiamato
Perciò, se ti vengono dati tre punti qualsiasi, puoi usare il circocentro per trovare un cerchio che passa da tutti e tre i punti. (A meno che i punti siano
Bisettici e cerchio inscritto
Comincerai probabilmente ad intuire il principio: scegliamo una costruzione, la ripetiamo tre volte per tutti i lati o angoli del triangolo, e poi scopriamo cos'ha di speciale l'intersezione di queste linee.
Ricorda che la
Ancora una volta, tutte e tre le linee si intersecano in un punto. Probabilmente te lo aspettavi, ma è importante notare che non è per niente ovvio che questo accada – i triangoli sono delle forme speciali!
I punti che giacciono su una bisettrice hanno la stessa distanza dalle due linee che delimitano l'angolo. Ad esempio, ogni punto sulla bisettrice blu ha la stessa distanza dal lato a e dal lato c, e ogni punto sulla bisettrice rossa ha la stessa distanza dai lati
Il punto di intersezione giace su tutte e tre le bisettrici. Perciò deve avere la stessa distanza da tutti e tre i
Questo significa che possiamo tracciare un cerchio attorno a questo punto, che si trova all'interno del triangolo e sfiora i suoi tre lati. Questo cerchio è chiamato cerchio inscritto al triangolo e il suo centro è detto incentro.
Area e altezze
Trovare l'area di un
La base del rettangolo corrisponde al lato inferiore del triangolo (che è chiamato base). L'altezza del rettangolo è la distanza perpendicolare tra la base e il vertice opposto.
L'altezza divide il triangolo in due parti. Nota come i due pezzi mancanti nel rettangolo hanno esattamente la stessa area delle due parti del triangolo. Questo significa che il rettangolo è grande
Possiamo facilmente calcolare l'area del rettangolo, quindi l'area di un triangolo deve valere la metà:
Per calcolare l'area di un triangolo, puoi scegliere uno qualsiasi dei tre lati come base, e poi trovare l'altezza corrispondente, che è la linea
Ogni triangolo possiede
Come per
Nei
Nei
Nei