Triangoli e trigonometriaIl teorema di Pitagora

Siamo ora arrivati ad un punto importante in geometria – essere in grado di formulare e capire uno dei più famosi teoremi di tutta la matematica: Il teorema di Pitagora. Prende il suo nome dal matematico greco Pitagora di Samo.

Il teorema di Pitagora In ogni triangolo rettangolo, il quadrato della lunghezza dell'ipotenusa (il lato che è opposto all'angolo retto) è pari alla somma dei quadrati degli altri due lati. In altre parole,

a2 + b2 = c2

Anche l'opposto è vero: se i tre lati di un triangolo soddisfano a*{sup}2* + b*{sup}2* = c*{sup}2*, allora il triangolo dev'essere .

Gli angoli retti si trovano ovunque, ecco perché il teorema di Pitagora è così utile.

Qui puoi vedere una scala che misura 6m appoggiata contro un muro. Il piede della scala dista 1m dal muro. Che altezza ragguinge la scala sul muro?

Nota che la scala, la parete e il pavimento formano un triangolo rettangolo. Usando il teorema di Pitagora otteniamo

h2+12	=62
⇒h2	=
⇒h	=35=5.92m

Ogni volta che ti trovi di fronte ad un triangolo rettangolo di cui conosci due lati, Pitagora ti può aiutare a trovare il terzo.

Dimostrare il teorema di Pitagora

Il teorema di pitagora era noto agli antichi Babilonesi, Sumeri, Indiani and Cinesi – ma Pitagora potrebbe essere stato il primo a trovarne una dimostrazione matematica formale.

Ci sono in realtà molti modi diversi di dimostrare il teorema di Pitagora. Puoi vedere qui tre esempi nei quali vengono usate tre diverse strategie:

Ridisposizione

Dai un'occhiata alla figura a destra. Il lato del quadrato misura a + b, e contiene quattro triangoli rettangoli, e un quadrato più piccolo di area .

Ora ridisponiamo i triangoli nel quadrato. La figura risultante contiene sempre i quatrro triangoli rettangoli, oltre a due quatrati di area .

Paragonando l'area in rosso prima e dopo la ridisposizione, vediamo che

a2+b2=c2.

Questa è la dimostrazione originale che Pitagora inventò.

c²

a²

b²

Algebra

Qui abbiamo la stessa figura di prima, ma questa volta useremo l'algebra anziché la ridisposizione per dimostrare il teorema di Pitagora.

Il quadrato grande ha lato a+b e area .

È composto da quattro triangoli, ognuno di area , e un quadrato di area .

Combinando queste informazioni, otteniamo

a+b2	=4×12ab+c2
a2+2ab+b2	=2ab+c2
a2+b2	=c2

E, ancora una volta, otteniamo il teorema di Pitagora.

Triangoli simili

Qui puoi vedere un altro triangolo rettangolo. Se tracciamo l'altezza relativa all'ipotenusa, essa dividerà il triangolo in due triangoli più piccoli. Dividerà anche l'ipotenusa c in due parti più piccole che chiameremo x e y. Continua

Separiamo ora i due triangoli più piccoli, per chiarire meglio cos'hanno in comune… Continua

Entrambi i triangoli più piccoli hanno un angolo in comune con il triangolo originale. Hanno anche un angolo retto. Secondo il criterio AA, tutti e tre i triangoli devono essere .

Ora possiamo usare le equazioni che già conosciamo per i poligoni simili:

xa=ac

x=a2c

yb=bc

y=b2c

Continua

Ma ricorda che c = x + y. Quindi:

c=a2c+b2c

c2=a2+b2

Ancora una volta, abbiamo dimostrato il teorema di Pitagora!

Molti aspetti della vita di Pitagora sono sconosciuti e nessuna copia originale del suo lavoro è pervenuta fino a noi. Fondò il culto religioso dei Pitagorici, che praticavano una sorta di “culto del numero”. Essi credevano che ogni numero avesse il proprio carattere e avevano una varietà di altre usanze bizzarre.

Ai Pitagorici vengono attribuite molte scoperte matematiche, inclusa la scoperta del primo numero irrazionale, 2. I numeri irrazionali non possono essere espressi come semplici frazioni – un concetto che i Pitagorici trovarono profondamente sconcertante e che cercarono (senza successo) di nascondere!

“Pitagorici che celebrano il sorgere del sole” by Fyodor Bronnikov

Calcolo delle distanze

Una delle applicazioni più importanti del teorema di Pitagora è il calcolo delle distanze.

A destra puoi vedere due punti in un sistema di coordinate. Potremmo misurare la loro distanza, ma la risposta non sarebbe perticolarmente accurata. Proviamo invece ad usare il teorema di Pitagora. Continua

Possiamo facilmente trovare la distanza orizzontale lungo l'asse x, e la distanza verticale lungo l'asse y. Se disegnamo queste due linee, otteniamo un triangolo rettangolo.

Usando Pitagora,

d2	=${b.x-a.x}2+${b.y-a.y}2
d2	=${(b.x-a.x)(b.x-a.x) + (b.y-a.y)(b.y-a.y)}
d	=${(b.x-a.x)2+(a.y-b.y)2}=${round(distance(a,b),4)}

Questo metodo funziona per_ogni_ coppia di punti:

La formula per la distanza Dati due punti con coordinate (x1,y1) e (x2,y2), la distanza tra di essi è

d2=x2−x12+y2−y12

d=x2−x12+y2−y12

Terne pitagoriche

Spostando i vertici del triangolo nel passaggio precedente, avrai forse notato che nella maggior parte dei casi, la lunghezza dell'ipotenusa d era . Tuttavia, ci sono alcuni esempi di triangoli rettangoli in cui la lunghezza di tutti e tre i lati risulta essere un numero intero.

Un esempio famoso è il triangolo 3-4-5 . Siccome 32+42=52, ogni triangolo con lati di lunghezza 3, 4 e 5 è rettangolo.

Gli antichi Egizi non conoscevano il teorema di Pitagora, ma conoscevano il triangolo 3-4-5 . Per costruire le piramidi, usavano corde annodate con lunghezze 3, 4 e 5 per formare angoli perfettamente retti.

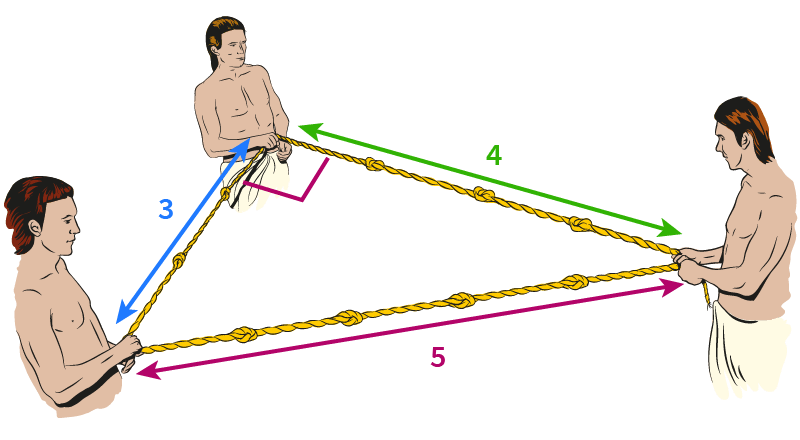
Tre numeri naturali come questi formano una terna pitagorica. (3, 4, 5) è un esempio di terna pitagorica. Se moltiplichiamo ogni numero per 2, otteniamo un'altra terna pitagorica: (6, 8, ).

Possiamo rappresentare queste terne con dei punti in un sistema di coordinate. Se la terna pitagorica è corretta, la distanza tra l'origine e il punto in questione dev'essere un numero intero. Usando il sistema di coordinate sotto, sapresti trovare altre terne pitagoriche?

${a.x}

${a.y}

${round(a.length,2)}

Noti una regolarità nella distribuzione di questi punti?

Cambia lingua

Accedi a Mathigon

Condividere

Ripristina avanzamento

Glossario